Current term (Fall 2024)
This term I’m an instructor for the course “Ordinary and Partial Differential Equations” (MATH 251) at Penn State. Further information about the course is available on the Canvas webpage.
Lecture notes for the course are available here:
Lecture notes Ordinary and Partial Differential Equations
Previous terms
Spring 2024
This term I was an instructor for the course “Calculus of Several Variables” (MATH 231) at Penn State. Further information about the course is available on the Canvas webpage.
Fall 2023
This term I was an instructor for the course “Calculus with Analytic Geometry II” (MATH 141) at Penn State. Further information about the course is available on the Canvas webpage.
Lecture notes for the course are available here:
Lecture notes Calculus with Analytic Geometry II
Spring 2023
This term I was an instructor for the course “Integral Calculus with Applications” (MATH 101) at UBC. Further information about the course is available on the Canvas webpage.
Here are some notes for the third-week class, concerning the substitution rule and the partial fraction decomposition.
This is an example, using GeoGebra, of implementation of the trapezoidal method to approximate definite integrals of functions whose values are only known at a given sample of points. Given a freehand-drawn function ![]() , the definite integral
, the definite integral ![]() is approximated with
is approximated with
![]()
![]()
See this spreadsheet for examples of numerical integration of
![]()
using Riemann sums, the trapezoidal method and Simpson’s rule at scale ![]() . The resulting expressions are given, respectively, by
. The resulting expressions are given, respectively, by
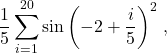
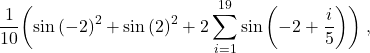
and
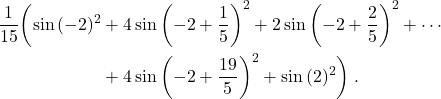
Week 6 class
First part: the logistic equation.
The logistic equation is a first-order differential equation describing a simple model of evolution of a population. It takes the following form:
(1) ![]()
where the unknown ![]() is a real-valued function of the time
is a real-valued function of the time ![]() . In accordance with our interpretation of the model, we shall only be interested in initial conditions of the form
. In accordance with our interpretation of the model, we shall only be interested in initial conditions of the form
![]()
We would like to understand the long-term behaviour of ![]() . To this end, we solve the differential equation in (1) using the method of separation of variables.
. To this end, we solve the differential equation in (1) using the method of separation of variables.
First, we examine separately the easiest possible solutions to the equation, represented by constant functions. A constant function ![]() ,
, ![]() , solves (1) if and only if
, solves (1) if and only if ![]() , that is, if and only if
, that is, if and only if ![]() (because of the constraint
(because of the constraint ![]() we have placed). Hence, the function which is constantly equal to
we have placed). Hence, the function which is constantly equal to ![]() is a solution to (1), corresponding to the initial condition
is a solution to (1), corresponding to the initial condition ![]() .
.
Remark: by a general theorem on existence and uniqueness of solutions to differential equations, it is the only function which solves (1) for the initial condition ![]() .
.
We may now assume that ![]() , and thus divide both sides of (1) by the right-hand side
, and thus divide both sides of (1) by the right-hand side ![]() , which by continuity of the function
, which by continuity of the function ![]() (solutions need to admit first derivatives, and hence are in particular continuous) is non-zero for
(solutions need to admit first derivatives, and hence are in particular continuous) is non-zero for ![]() close to the initial time
close to the initial time ![]() . We get
. We get
(2) ![]()
taking antiderivatives (that is, indefinite integrals) on both sides, this is equivalent to
(3) ![]()
On the one hand, we obviously have
![]()
![]()
where the last equality follows from the method of partial fractions, observing that the equation
![]()
in the unknowns ![]() and
and ![]() is solved for
is solved for ![]() .
.
Since ![]() and
and ![]() , with
, with ![]() , we deduce that (3) holds if and only if
, we deduce that (3) holds if and only if
(4) ![]()
Remark: strictly speaking, we have
![]()
but we incorporate the constant ![]() into
into ![]() to ease notation in (4).
to ease notation in (4).
Now (4) is equivant, taking exponentials on both sides, to
![]()
removing the absolute values, the latter amounts to
![]()
calling ![]() , so that
, so that ![]() can be any non-zero real number. It remains to solve the previous equation for
can be any non-zero real number. It remains to solve the previous equation for ![]() :
:
![]()
which yields
![]()
Dividing numerator and denominator by the non-zero quantity ![]() , we get the simplified expression
, we get the simplified expression
(5) ![]()
for the solution, where we have set ![]() .
.
Notice that we recover the constant solution ![]() , singled out at the beginning, by allowing
, singled out at the beginning, by allowing ![]() to be equal to
to be equal to ![]() . Furthermore, imposing the initial condition
. Furthermore, imposing the initial condition ![]() in (5) allows to determine
in (5) allows to determine ![]() in terms of
in terms of ![]() . Indeed, we get
. Indeed, we get
![]()
We have reached the following conclusion: the general solution to the logistic equation (1) with strictly positive initial conditions is given by
![]()
We now examine the limit of ![]() , as given in the last displayed formula, as
, as given in the last displayed formula, as ![]() tends to
tends to ![]() . Since
. Since ![]() , we have
, we have
![]()
irrespective of the value of
Second part: the logistic equation with proportional harvesting.
The logistic equation with proportional harvesting is obtained from the logistic equation by adding a factor which takes into account the consumption of resources of the environment, assumed to be proportional to the number of individuals of the population. It takes the form
(6) ![]()
where ![]() is a constant of proportionality.
is a constant of proportionality.
In order to understand the asymptotic behaviour of the solutions, where we again assume that the initial condition is ![]() , we proceed exactly in the same way as for the logistic equation. Before turning to actual computations, observe that it is reasonable to surmise that, in view of the additional consumption of resources, the environment will not allow an equilibrium state equal to
, we proceed exactly in the same way as for the logistic equation. Before turning to actual computations, observe that it is reasonable to surmise that, in view of the additional consumption of resources, the environment will not allow an equilibrium state equal to ![]() any longer; if
any longer; if ![]() is sufficiently small, we might guess that there will still be an equilibrium state for the system, which is strictly smaller than
is sufficiently small, we might guess that there will still be an equilibrium state for the system, which is strictly smaller than ![]() , whereas if
, whereas if ![]() is large enough we might predict that the population eventually dies out. We shall see that this is precisely the case.
is large enough we might predict that the population eventually dies out. We shall see that this is precisely the case.
First, we deal with possible constant solutions. A function ![]() which is constantly equal to a certain value
which is constantly equal to a certain value ![]() solves (6) if and only if
solves (6) if and only if ![]() is a root of the polynomial (in the variable
is a root of the polynomial (in the variable ![]() )
) ![]() , that is, if and only if
, that is, if and only if ![]() or
or ![]() . As we disregard the initial conditions
. As we disregard the initial conditions ![]() , this yields the only value
, this yields the only value ![]() . Therefore,
. Therefore, ![]() is the unique constant function solving (6) for an initial condition
is the unique constant function solving (6) for an initial condition ![]() .
.
Assuming now ![]() , we can divide both sides of (6) by the right-hand side
, we can divide both sides of (6) by the right-hand side ![]() , which is non-zero by continuity for
, which is non-zero by continuity for ![]() sufficiently close to
sufficiently close to ![]() : we thus get
: we thus get
![]()
Taking indefinite integrals, the previous equality is verified if and only
(7) ![]()
where
First case: ![]() . In this case
. In this case ![]() is an antiderivative of
is an antiderivative of ![]() , so that we can take
, so that we can take ![]() . Therefore, (7) is equivalent to
. Therefore, (7) is equivalent to
![]()
which amounts to
![]()
Plugging the initial condition
![]()
We deduce that
![]()
for every initial condition
Seeond case: ![]() . We apply the method of partial fractions and decompose
. We apply the method of partial fractions and decompose
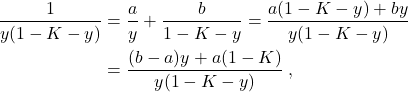
where we need to find
![]()
![]()
Equality
![]()
is thereby equivalent to
![]()
We now solve the previous equation for
![]()
implies, multiplying both sides by
![]()
Calling
![]()
which amounts to
![]()
that is, to
(8) ![]()
where the last equality follows by dividing numerator and denominator by the nonzero quantity ![]() and calling
and calling ![]() . Observe that, when
. Observe that, when ![]() is allowed to be equal to
is allowed to be equal to ![]() , we recover the constant solution
, we recover the constant solution ![]() examined at the beginning.
examined at the beginning.
Plugging the initial condition ![]() in (8), we get
in (8), we get
![]()
from which we readily find
![]()
Finally, we conclude that the unique solution to (6) (for
![]()
Now observe that we have different asymptotic behaviours of the solution, depending on whether ![]() is larger or smaller than
is larger or smaller than ![]() . If
. If ![]() , then
, then
![]()
from which it follows that
![]()
for every initial condition ![]() . On the other hand, if
. On the other hand, if ![]() , then
, then
![]()
so that
![]()
for every initial condition ![]() .
.
To sum up, our analysis has brought to the fore the presence of three distinct regimes for the logistic equation with proportional harvesting.
- In the case
 , the evolution does not involve an overwhelming consumption of resources, so that the system allow an equilibrium state at the value
, the evolution does not involve an overwhelming consumption of resources, so that the system allow an equilibrium state at the value 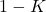 , to which every solution tends asymptotically. Observe that, consistently with the underlying intuition, the very fact that there is consumption of resources (
, to which every solution tends asymptotically. Observe that, consistently with the underlying intuition, the very fact that there is consumption of resources (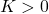 ) corresponds to the equilibrium state
) corresponds to the equilibrium state 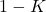 being strictly smaller than the corresponding one for the logistic equation without harvesting.
being strictly smaller than the corresponding one for the logistic equation without harvesting. - At the value
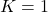 , a phase transition occurs for the given model: the population does not stabilise towards a positive value any longer, but instead dies out irrespective of the initial number of individuals. Furthermore, the explicit expression of the solution enables us to understand that the rate of decay of the number of individuals is polynomial, that is,
, a phase transition occurs for the given model: the population does not stabilise towards a positive value any longer, but instead dies out irrespective of the initial number of individuals. Furthermore, the explicit expression of the solution enables us to understand that the rate of decay of the number of individuals is polynomial, that is, 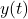 tends to zero with the same speed as the function
tends to zero with the same speed as the function 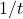 .
. - Finally, in the case
 , the population eventually dies out once again. However, if the qualitative behaviour of the solution
, the population eventually dies out once again. However, if the qualitative behaviour of the solution 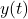 (namely the fact that it tends to
(namely the fact that it tends to 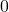 ) matches the case
) matches the case 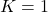 , the quantitative behaviour substantially tells the two cases apart. Indeed, in this case,
, the quantitative behaviour substantially tells the two cases apart. Indeed, in this case, 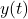 tends towards the limiting value
tends towards the limiting value 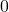 with the same speed as the function
with the same speed as the function 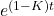 , hence much faster than
, hence much faster than 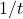 does; in other words, the rate of decay is exponential.
does; in other words, the rate of decay is exponential.
Here are the phase lines both for the standard logistic equation and for the logistic equation with proportional harvesting. Observe that, from a qualitative perspective, the asymptotic behaviour of the solutions can be entirely read off from the phase line, without solving the equation explicitly. However, finer information such as the speed of convergence to equilibria cannot be inferred from the phase line.
Past courses
This is a list of the courses and seminars for which I was teaching assistant in the last five years at ETH:
- Fall 2021 – Student seminar: Elementary Number Theory
- Fall 2020 – Algebraic Geometry I
- Fall 2020 – Differential Geometry 1
- Fall 2019 – Student seminar: Homogeneous Dynamics and Counting Problems
- Fall 2019 – Analysis III: Partial Differential Equations
- Spring 2019 – Functional Analysis II
- Fall 2018 – Functional Analysis I
- Fall 2018 – Commutative Algebra
- Fall 2017 – Linear Algebra
During the academic year 2021-2022 I co-organized the Geometry Graduate Colloquium in the mathematics department at ETH: the webpage is here.
